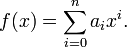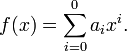viernes, 24 de junio de 2011
rompecabezas mil piezas
recordando; traslación de función
y = f (x) una función. La función y = f (x - h) es la función f (x) trasladada h unidades en horizontal. Si >0 el desplazamiento es hacia la derecha y si h<0 es hacia la izquierda. = sin( x - p ) es la función y = sin x desplazada p unidades hacia la derecha = sin( x - p ) = sin x La función y = f (x) + k es la función f (x) desplazada k unidades en vertical. Sik>0 el desplazamiento es hacia arriba y si k<0 el desplazamiento es hacia
Sea
·
h
y
y
y
·
encuentra la función inversa y gráfica
Se llama función inversa o reciproca de f a otra función f−1 que cumple que:
Si f(a) = b, entonces f−1(b) = a.

Podemos observar que:
El dominio de f−1 es el recorrido de f.
El recorrido de f−1 es el dominio de f.
Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.
Si dos funciones son inversas su composición es la función identidad.
f o f -1 = f -1 o f = x
Las gráficas de f y f -1 son simétricas respecto de la bisectriz del primer y tercer cuadrante.

Hay que distinguir entre la función inversa, f−1(x), y la inversa de una función,  .
.
actividad 4 describe en forma geométrica y aritmética la inversa de una función
Se ha modificado la actividad de potencias, dividiéndose en tres apartados, potencias de números naturales, enteros y reales. Cada uno de estos apartados se subdivide a su vez teniendo en cuenta las distintas operaciones
actividad 3 problemas de capital y crecimiento de población
La República de Honduras, esta limitada al Norte por el Atlántico, al Este por el mismo mar y la República de Nicaragua, al Sur por Nicaragua, el Golfo de Fonseca y la República de El Salvador, y al Oeste la República de Guatemala. La extensión territorial de Honduras, comprendiendo todas sus islas,[4] es de aproximadamente 112.492 km².[5]
Honduras se divide en 18 departamentos. Las ciudades de Tegucigalpa y Comayagüela, conjuntamente, constituyen la capital de la república.[1] La forma de gobierno es republicana, democrática y representativa. Se ejerce por tres poderes: Legislativo, Ejecutivo y Judicial, complementarios e independientes y sin relaciones de subordinación.[6] [7]
La población de Honduras es de 8+ millones de habitantes,[8] y está entre las que registra un mayor número de crecimiento en Latinoamérica. [9] [10] Los hondureños se dedican en su mayor parte a las actividades agropecuarias, además del comercio, manufacturas, finanzas, y servicios públicos entre otras actividades. El departamento de Honduras con mayor densidad de población es Cortés con 400.3 hab./km².[8] El país es multiétnico, consta de cuatro grandes familias étnicas: los ladinos o mestizos
Honduras se divide en 18 departamentos. Las ciudades de Tegucigalpa y Comayagüela, conjuntamente, constituyen la capital de la república.[1] La forma de gobierno es republicana, democrática y representativa. Se ejerce por tres poderes: Legislativo, Ejecutivo y Judicial, complementarios e independientes y sin relaciones de subordinación.[6] [7]
La población de Honduras es de 8+ millones de habitantes,[8] y está entre las que registra un mayor número de crecimiento en Latinoamérica. [9] [10] Los hondureños se dedican en su mayor parte a las actividades agropecuarias, además del comercio, manufacturas, finanzas, y servicios públicos entre otras actividades. El departamento de Honduras con mayor densidad de población es Cortés con 400.3 hab./km².[8] El país es multiétnico, consta de cuatro grandes familias étnicas: los ladinos o mestizos
actividad en el salón
Funciones y su representación gráfica
Introducción:
En los diseños curriculares se aprecia una constante preocupación por que los alumnos adquieran los conocimientos necesarios para desenvolverse como ciudadanos capaces de ejercer sus derechos y deberes en una sociedad que incorpora cada vez más a su funcionamiento, a sus actividades y a sus lenguajes ciertos aspectos matemáticos.
En los diseños curriculares se aprecia una constante preocupación por que los alumnos adquieran los conocimientos necesarios para desenvolverse como ciudadanos capaces de ejercer sus derechos y deberes en una sociedad que incorpora cada vez más a su funcionamiento, a sus actividades y a sus lenguajes ciertos aspectos matemáticos.
como se calcula el crecimiento de población
18. ¿Cómo se mide el crecimiento de la población? El crecimiento poblacional se mide, por lo general, mediante el empleo de una ecuación matemática que describe el cambio ocurrido en un determinado período, en el supuesto de que la tendencia experimentada ha sido la de una línea recta, una curva geométrica, o una curva exponencial. 19.¿Cuales son los supuestos del crecimiento aritmético y geométrico de la población? El crecimiento aritmético supone un crecimiento lineal o sea que cada año la población crece en una magnitud constante, por lo que su utilización es aconsejable solamente en períodos cortos (6 meses, 1 o 2 años). El crecimiento geométrico supone un crecimiento porcentual constante en el tiempo, es aplicable en períodos largos, lo que desde el punto de vista demográfico se identifica más con el comportamiento real de la población. 20. ¿Cómo se interpreta el crecimiento lineal o aritmético de la población? El empleo de una línea recta para medir el cambio poblacional, supone que la población ha aumentado (o disminuido) en una cantidad promedio constante durante todo el período de observación. La ecuación que describe este tipo de crecimiento es la siguiente: y puede medirse a partir de una tasa promedio anual de crecimiento, cuya aproximación aritmética sería la siguiente: donde: del período 21. ¿Cómo se interpreta el crecimiento geométrico y que nos muestra? Mediante el empleo de una curva de este tipo, se asume que la población crece (o decrece) a una misma tasa promedio en cada unidad de tiempo, usualmente un año. Este tipo de crecimiento se describe a partir de la siguiente ecuación: donde "r" es la tasa de crecimiento promedio anual (constante) del período y puede calcularse de la siguiente forma: aplicando logaritmos, a fin de facilitar el cálculo: |
22. ¿A que se refiere el cambio exponencial? Con la aplicación de una curva de tipo exponencial, se asume una tasa de crecimiento que se aplica a la población en cada infinitésimo de tiempo. A diferencia del crecimiento geométrico, que implica una acumulación de población en forma anual, en este caso la acumulación es instantánea. La ecuación que expresa dicho crecimiento es : donde " i " es la tasa de crecimiento instantánea y se calcula de la siguiente forma: donde: N0 y Nt : población al inicio y al final del período, respectivamente, log e : 0,434294 La tasa de crecimiento, calculada a partir de cualquiera de las anteriores fórmulas, se expresa por lo general en forma porcentual, para ello se multiplica por 100. El tiempo " t " se mide en años, siendo recomendable usar hasta 4 decimales si el período se expresa en años, meses y días. Esto ocurre con frecuencia cuando se quiere calcular la tasa de crecimiento de un período intercensal, por ejemplo, el período comprendido entre los censos de 1981 y 1993, que transcurre entre el 12 de julio de 1981 y el 11 de julio de 1993. En este caso t =11.9973 años. Ejemplo: Dados los volúmenes de la población peruana, estimados al 30 de junio de los años 1950,1960, 1970, y 1980. Se pide determinar las tasas de crecimiento promedio anual entre dichas fechas, asumiendo una tendencia lineal, geométrica y exponencial de la población. Población 1950 7632,5 Población 1960 9931,0 Población 1970 13192,8 Población 1980 17295,3 Solución aplicando las fórmulas para el período 1950-60, se tiene: Siguiendo la tendencia Lineal |
como se calcula el interés compuesto
Puedes tanto haber hecho una compra o una inversión mayor, o pagado o recibido un interés compuesto. La mayoría de las personas, no obstante, desconocen cómo el banco calcula la cantidad que debe cargar o pagar cada mes
Lee mas en: http://www.enplenitud.com/nota.asp?notaid=10242#ixzz1QEq8KYwv
Descarga libros gratis en http://www.enplenitud.com/libros
Lee mas en: http://www.enplenitud.com/nota.asp?notaid=10242#ixzz1QEq8KYwv
Descarga libros gratis en http://www.enplenitud.com/libros
realiza las siguientes actividades
MamutMatematicas.com tiene varias generadores que pueden realizarte un gran variedad de hojas de ejercicios y problemas de matemáticas.
Puede seleccionar entre distintas opciones para hacerlas tan fácil o difícil como el nivel del alumno, con más ejercicios o menos, letra grande o pequeña, etcetera.
Mientras que son generadas aleatoriamente, realizas cada vez una hoja de ejercicios distintos. Escoja una tema del menú que sigue:
Puede seleccionar entre distintas opciones para hacerlas tan fácil o difícil como el nivel del alumno, con más ejercicios o menos, letra grande o pequeña, etcetera.
Mientras que son generadas aleatoriamente, realizas cada vez una hoja de ejercicios distintos. Escoja una tema del menú que sigue:
sistema de medidas para líquidos superficie y volumen
El volumen es una magnitud escalar definida como el espacio ocupado por un cuerpo. Es una función derivada ya que se halla multiplicando las tres dimensiones.
En matemáticas el volumen es una medida que se define como los demás conceptos métricos a partir de una distancia o tensor métrico.
En física, el volumen es una magnitud física extensiva asociada a la propiedad de los cuerpos físicos de ser extensos, que a su vez se debe al principio de exclusión de Pauli.
La unidad de medida de volumen en el Sistema Internacional de Unidades es el metro cúbico, aunque temporalmente también acepta el litro, que se utiliza comúnmente en la vida práctica
En matemáticas el volumen es una medida que se define como los demás conceptos métricos a partir de una distancia o tensor métrico.
En física, el volumen es una magnitud física extensiva asociada a la propiedad de los cuerpos físicos de ser extensos, que a su vez se debe al principio de exclusión de Pauli.
La unidad de medida de volumen en el Sistema Internacional de Unidades es el metro cúbico, aunque temporalmente también acepta el litro, que se utiliza comúnmente en la vida práctica
derivada
En cálculo (rama de las matemáticas), la derivada se representa cómo una función que cambia (valor de la variable dependiente) a medida que su entrada (valor de la variable independiente) cambia. En términos poco rigurosos, una derivada puede ser vista como cuánto está cambiando el valor de una función en un punto dado (o sea su velocidad de variación); por ejemplo, la derivada de la posición de un vehículo con respecto al tiempo, es la velocidad instantánea con la cual el vehículo está viajando.
La derivada de una función es un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas
La derivada de una función es un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas
investigar las propiedades de las curvas en una función
En microeconomía las curvas de indiferencia se definen como los conjuntos de puntos en el espacio de combinaciones de bienes para los que la satisfacción del consumidor es idéntica, es decir que para todos los puntos pertenecientes a una misma curva, el consumidor no tiene preferencia por la combinación representada por uno sobre la combinación representada por otro. La satisfacción del consumidor se caracteriza mediante la función de utilidad en la que las variables son las cantidades de cada bien representadas por el valor sobre cada eje.
Existen discrepancias entre autores sobre si la continuidad, derivabilidad y convexidad de dichas curvas están garantizadas y ello tiene fuertes implicaciones en al discusión de la existencia o no de puntos de equilibrio. Desde un punto de vista matemático la discusión implica el axioma de elección.
Existen discrepancias entre autores sobre si la continuidad, derivabilidad y convexidad de dichas curvas están garantizadas y ello tiene fuertes implicaciones en al discusión de la existencia o no de puntos de equilibrio. Desde un punto de vista matemático la discusión implica el axioma de elección.

función racionales asíntotas
La asíntotas son rectas a las cuales se aproxima una función sin llegar a ellas.
3 + x D ={- 3 } x = - 3
2) Asíntota vertical es el valor que no pertenece al dominio de la función, pero tampoco la anula.
lim 1 1 = 1 = ∞
3 + x 3 - 3 0
x → -3

lim x → ∞ 1
x
= 0 = 0 = 0
3 + x 1 + 0 1
x x
Asíntota horizontal = 0
Intersección con el eje x y = 0
1 = 0
3 + x
1 = 0 . (3 + x)
1 = 0
No existe
Intersección con el eje y x = 0
1 = 1 = 1 = 0,33...
3 + x 3 + 0 3
( 0 ; 0,33..)
( - ∞ ; - 3)
( - 3 ; 0)
(0 ; + ∞)
 1 =
1 =
x
1 = ∞
0
x→ 0
1 = 0
x
x→∞
Ejemplos:
La asíntota horizontal es igual a 01) Dominio
f(x) = 1 3 + x = 0 3 + x D ={- 3 } x = - 3
2) Asíntota vertical es el valor que no pertenece al dominio de la función, pero tampoco la anula.
lim 1 1 = 1 = ∞
3 + x 3 - 3 0
x → -3

3)
Asíntota horizontallim x → ∞ 1
x
= 0 = 0 = 0
3 + x 1 + 0 1
x x
Asíntota horizontal = 0
Intersección con el eje x y = 0
1 = 0
3 + x
1 = 0 . (3 + x)
1 = 0
No existe
Intersección con el eje y x = 0
1 = 1 = 1 = 0,33...
3 + x 3 + 0 3
( 0 ; 0,33..)
( - ∞ ; - 3)
( - 3 ; 0)
(0 ; + ∞)
- - - - - - - - - - - - - -

x
1 = ∞
0
x→ 0
1 = 0
x
x→∞
x | y = 1/x |
- 3 | - 0,3333.. |
- 2 | - 0,5 |
- 1 | - 1 |
0 | ∞ |
1 | 1 |
2 | 0,5 |
3 | 0,333 |
; grafica las siguientes expresiones
La expresión grafica y el dibujo libre
Toda expresión grafica, dibujos, escrituras, constituyen una herramienta de comunicación, conocimiento, exploración, y evaluación valiosa cuando tenemos como objetivo acceder a los dinamismos psíquicos, consientes e inconscientes de un individuo o de uno de ellos.
El contenido de lo que me propongo en este articulo es pensar y reflexionar acerca de la lectura que hacemos cuando tenemos frente a nosotros una producción grafica, dibujos realizados con o sin intención (garabatos, producciones espontaneas y personales de un sujeto) esto implica el considerar cual es el objetivo de nuestra mirada si persigue algún fin en particular.
El segundo propósito es el reflexionar acerca de la técnica del dibujo libre. A mi modo de ver en primer lugar cuando encaramos nuestra profesión el abordaje de una producción grafica podemos hacerlo con múltiples intenciones, la mas usual es con fines psicodiagnostico es decir, explorar a través de las producciones de un sujeto determinado, características generales o especificas de su personalidad y aquí surge un primer recorte, ya que la evaluación que hagamos no siempre debe ser completa y de ello depende del objetivo que persiga el psicodiagnostico, esto puede responder a tres orientaciones que son las siguientes:
Toda expresión grafica, dibujos, escrituras, constituyen una herramienta de comunicación, conocimiento, exploración, y evaluación valiosa cuando tenemos como objetivo acceder a los dinamismos psíquicos, consientes e inconscientes de un individuo o de uno de ellos.
El contenido de lo que me propongo en este articulo es pensar y reflexionar acerca de la lectura que hacemos cuando tenemos frente a nosotros una producción grafica, dibujos realizados con o sin intención (garabatos, producciones espontaneas y personales de un sujeto) esto implica el considerar cual es el objetivo de nuestra mirada si persigue algún fin en particular.
El segundo propósito es el reflexionar acerca de la técnica del dibujo libre. A mi modo de ver en primer lugar cuando encaramos nuestra profesión el abordaje de una producción grafica podemos hacerlo con múltiples intenciones, la mas usual es con fines psicodiagnostico es decir, explorar a través de las producciones de un sujeto determinado, características generales o especificas de su personalidad y aquí surge un primer recorte, ya que la evaluación que hagamos no siempre debe ser completa y de ello depende del objetivo que persiga el psicodiagnostico, esto puede responder a tres orientaciones que son las siguientes:
funciones polinomiales de 3 grado y 4 grad
Polinomio, en matemáticas, se denomina a la suma de varios monomios, llamados términos del polinomio. Es una expresión algebraica constituida por una o más variables, utilizando solamente operaciones de adición, sustracción, multiplicación y exponentes numéricos positivos. El polinomio de un sólo término se denomina monomio, el de dos binomio, el de tres trinomio.
La expresión general de los polinomios que sólo tienen una variable, los más utilizados, es:
por ejemplo:
Se denomina grado de un polinomio al mayor de los grados de los monomios que lo componen.
Historia [editar]
Volumen de una pirámide truncada.La resolución de ecuaciones algebraicas, o la determinación de las raíces de polinomios, está entre los problemas más antiguos de la matemática. Sin embargo, la elegante y práctica notación que utilizamos actualmente se desarrolló a partir del siglo XV.
En el problema 14º del papiro de Moscú (ca. 1890 a. C.) se pide calcular el volumen de un tronco de pirámide cuadrangular. El escriba expone los pasos: eleva al cuadrado 2 y 4, multiplica 2 por 4, suma los anteriores resultados y multiplícalo por un tercio de 6 (h); finaliza diciendo: «ves, es 56, lo has calculado correctamente». En notación algebraica actual sería: V = h (t² + b² + tb) / 3, un polinomio de cuatro variables (V, h, t, b) que, conociendo tres, permite obtener la cuarta variable.
Algunos polinomios, como f(x) = x² + 1, no tienen ninguna raíz que sea número real. Sin embargo, si el conjunto de las raíces posibles se extiende a los números complejos, todo polinomio (no constante) tiene una raíz: ese es el enunciado del teorema fundamental del álgebra.
Hay una diferencia entre la aproximación de raíces y el descubrimiento de fórmulas concretas para ellas. Se conocen fórmulas de polinomios de hasta cuarto grado desde el siglo XVI (ver ecuación cuadrática, Gerolamo Cardano, Niccolo Fontana Tartaglia). Pero, las fórmulas para polinomios de quinto grado fueron irresolubles para los investigadores durante mucho tiempo. En 1824, Niels Henrik Abel demostró que no puede haber fórmulas generales para los polinomios de quinto grado o mayores (ver el teorema de Abel-Ruffini). Este resultado marcó el comienzo de la teoría de Galois que se ocupa del estudio detallado de las relaciones existentes entre las raíces de los polinomios.
La máquina diferencial de Charles Babbage fue diseñada para crear automáticamente tablas de valores de funciones logarítmicas y diferenciales, evaluando aproximaciones polinómicas en muchos puntos, usando el método de las diferencias de Newton.
Funciones polinómicas [editar]Las funciones polinómicas son aquellas que surgen de evaluar los polinomios sobre las variables en las que están definidos. Son una clase de funciones suaves, esto es, son infinitamente diferenciables (tienen derivadas de todos los órdenes finitos).
A las funciones polinómicas de
Función polinómica de grado 0, que también se denomina: funciones constantes
Función polinómica de grado 1, que también se denomina: funciones lineales,
Función polinómica de grado 2, que también se denomina: funciones cuadráticas,
Función polinómica de grado 3, que también se denomina: funciones cúbicas.
Función polinómica de grado 4
Debido a su estructura simple, los polinomios son muy sencillos de evaluar, y se usan ampliamente en análisis numérico para interpolación polinómica o para integrar numéricamente funciones más complejas. Una manera muy eficiente para evaluar polinomios es la utilización de la regla de Horner.
En álgebra lineal el polinomio característico de una matriz cuadrada codifica muchas propiedades importantes de la matriz. En teoría de los grafos el polinomio cromático de un grafo codifica las distintas maneras de colorear los vértices del grafo usando x colores.
Con el desarrollo de la computadora, los polinomios han sido remplazados por funciones spline en muchas áreas del análisis numérico. Las splines se definen a partir de polinomios y tienen mayor flexibilidad que los polinomios ordinarios cuando definen funciones simples y suaves. Éstas son usadas en interpolación spline y gráficos por ordenador.
Definición algebraica [editar]Para a0, …, an constantes en algún anillo (en particular podemos tomar un cuerpo, como o , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
El polinomio se puede escribir más concisamente usando sumatorios como
Las constantes a0, …, an se llaman los coeficientes del polinomio. A a0 se le llama el coeficiente constante y a an, el coeficiente principal. Cuando el coeficiente principal es 1, al polinomio se le llama mónico o normado. Siendo x un símbolo llamado indeterminada.
Operaciones con polinomios [editar]Artículo principal: Operaciones con polinomios
Los polinomios se pueden sumar y restar agrupando los términos y simplificando los monomios semejantes. Para multiplicar polinomios se multiplica cada término de un monomio por el término del otro monomio y se simplifican los monomios semejantes, posteriormente.
Factorización [editar]Artículo principal: Factorización
Para factorizar un polinomio de segundo grado completo (con todos los términos) se divide por el inverso de una de sus raíces sumado con la incógnita, siendo los factores el número por el que dividimos y el resultado; ya que no hay resto, cumpliendose así que dividendo = divisor Χ cociente + resto. En caso de que el polinomio no tenga término independiente se sacará la incógnita como factor común y ya está factorizado. También se puede factorizar usando las igualdades notables.
Ejemplos [editar]Las funciones polinómicas de una variable (x), se corresponden con diversas curvas planas, que se pueden representar en un sistema de coordenadas cartesianas XY.
Polinomio de grado 2:
f(x) = x2 - x - 2 = (x+1)(x-2)
Polinomio de grado 3:
f(x) = x3/5 + 4×2/5 - 7x/5 - 2 = 1/5 (x+5)(x+1)(x-2)
Polinomio de grado 4:
f(x) = 1/14 (x+4)(x+1)(x-1)(x-3) + 0.5
Polinomio de grado 5:
f(x) = 1/20 (x+4)(x+2)(x+1)(x-1)(x-3) + 2
Estimado Maestro o profesional del area te invito a colaborar construyendo este sitio aportando el material apropiado ( de preferencia usando los formatos de competencias digitales aqui descritos ) y/o tambien competencias genericas o especificas a cada uno de los mas de 2,000 temas que lo compone es un esfuerzo personal y de muchos maestros y amigos de MEXICO y el Mundo Hispano por devolver algo de lo mucho que hemos recibido en el proceso de la educacion preparatoria,
Solo usar la opcion de EDIT abajo en esta pagina y entrar a un editor de texto, para beneficio de todos los interesados en la preparatoria y bachillerato en Mexico.
Mucho agradecere tu aportacion y colaboracion, un afectuoso saludo Prof Lauro Soto, Ensenada, BC, Mexico.
; para qué sirve la derivada

El concepto de derivada es uno de los dos conceptos centrales del cálculo infinitesimal. El otro concepto es la «antiderivada» o integral; ambos están relacionados por el teorema fundamental del cálculo. A su vez, los dos conceptos centrales del cálculo están basados en el concepto de límite, el cual separa las matemáticas previas, como el Álgebra, la Trigonometría o la Geometría Analítica, del Cálculo. Quizá la derivada es el concepto más importante del Cálculo Infinitesimal.
que es derivar
En cálculo (rama de las matemáticas), la derivada se representa cómo una función que cambia (valor de la variable dependiente) a medida que su entrada (valor de la variable independiente) cambia. En términos poco rigurosos, una derivada puede ser vista como cuánto está cambiando el valor de una función en un punto dado (o sea su velocidad de variación); por ejemplo, la derivada de la posición de un vehículo con respecto al tiempo, es la velocidad instantánea con la cual el vehículo está viajando.
La derivada de una función es un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas
La derivada de una función es un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas
funciones polinomiales de grado 2 y las particularidades de los modelos cuadráticos
ecuaciones cuadráticas pueden tomar tres formas útiles: La forma de vértice es y a(x h)2 k. Esta forma es útil para decir cómo lay x2 ha sido transformada. El vértice (h, k) de la parábola es ela dice la cantidad de estiramiento vertical,a revela una reflexión alrededor del eje x. La forma factorizada es y a(x x1)(x x2). De esta forma es fácil decir que lasx1 y x2 y que la gráfica tiene intersecciones x en x1 y x2. La forma general es y ax2 bx c. Esta forma es útil para hallar que lay es c—la parábola cruza el eje y en (0, c). Si la ecuación describe laa es la mitad de la aceleraciónb es la velocidad inicial y c es la altura inicial por encima
Las
●
gráfica madre
punto más alto o más bajo. El factor
y un valor negativo de
●
raíces de la ecuación son
●
intersección
altura de un objeto que sube o cae, entonces
debida a la gravedad,
del nivel del suelo
examen prueba en línea.
Contesta por tu propia cuenta la prueba ENLACE que está disponible “en línea” y el resultado te será proporcionado de forma inmediata aquí mismo. Comienza seleccionando un grado escolar
linea recta
En geometría euclidiana, la recta o línea recta, es el ente ideal que se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, o sea, no posee principio ni fin.
Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición sólo es posible a partir de la descripción de las características de otros elementos similares. Así, es posible elaborar definiciones basándose en los Postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.
Las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.
En geometría euclidiana, la recta o línea recta, es el ente ideal que se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, o sea, no posee principio ni fin.
Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición sólo es posible a partir de la descripción de las características de otros elementos similares. Así, es posible elaborar definiciones basándose en los Postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.
Las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.
Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición sólo es posible a partir de la descripción de las características de otros elementos similares. Así, es posible elaborar definiciones basándose en los Postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.
Las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.
En geometría euclidiana, la recta o línea recta, es el ente ideal que se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, o sea, no posee principio ni fin.
Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición sólo es posible a partir de la descripción de las características de otros elementos similares. Así, es posible elaborar definiciones basándose en los Postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.
Las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.
funciones polinomiales de grado
En matemática, las funciones polinómicas son las funciones

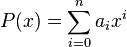

- donde
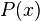 es un polinomio en
es un polinomio en  ,
, 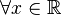 , es decir, una suma finita de potencias de
, es decir, una suma finita de potencias de  multiplicados por coeficientes reales, de la forma:
multiplicados por coeficientes reales, de la forma:
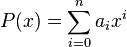
función polinomiales de grado cero, uno, y dos
Funciones polinomiales - Document Transcript
- 9 Funciones polinómicas Objetivos Antes de empezar. En esta quincena aprenderás a: 1.Funciones polinómicas ................ pág. 150 • Distinguir entre los distintos Características tipos de funciones cuya gráfica es una recta y trabajar con 2.Funciones de primer grado .......... pág. 151 ellas. Término independiente Coeficiente de grado uno • Determinar la pendiente de una Recta que pasa por dos puntos recta y su relación con el crecimiento. Aplicaciones • Calcular la ecuación de una 3.Funciones de segundo grado ........ pág. 154 recta que pasa por dos puntos La parábola y=x2 dados. Traslaciones de una parábola. • Reconocer la gráfica de una Representar funciones cuadráticas función polinómica de segundo Aplicaciones grado cualquiera. Ejercicios para practicar • Representar gráficamente una función polinómica de segundo grado y=ax2+bx+c. Para saber más • Determinar el crecimiento o Resumen decrecimiento de una función de segundo grado y hallar su máximo o mínimo. Autoevaluación Actividades para enviar al tutor MATEMÁTICAS B 147
; traslaciones verticales y horizontales
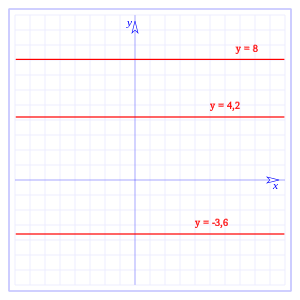
¿Cómo comparas las gráficas de y = x2 + 2 y y = x2 - 3 con la gráfica de y = x2? Observa las gráficas a continuación.
Observa que la gráfica de y = x2 + 2 sube dos unidades desde el origen y la gráfica de y = x2 - 3 baja tres unidades desde el origen.
Nota: La gráfica de la ecuación de la forma y = f(x) + k es la gráfica de y = f(x) desplazada hacia arriba si k es positiva y desplazada hacia abajo si k es negativa. De manera que, la gráfica de y = f(x) + k se puede obtener de la gráfica de y = f(x) al trasladar verticalmente la gráfica de y = f(x), k unidades hacia arriba si k es positiva y k unidades hacia abajo si k es negativa.
Traslación horizontal
¿Cómo comparas las gráficas de y = (x + 2)2 y y = (x - 2)2 con la gráfica de y = x2? Observa las gráficas a continuación.
Observa que la gráfica de y = ( x + 2)2 se mueve dos unidades hacia la izquieda y la gráfica de y = (x - 2)2 se mueve dos unidades hacia la derecha.
Nota: La gráfica de y = f(x + h) es la gráfica de y = f(x) desplazada hacia la derecha si h es negativa y desplazada hacia la izquierda si h es positiva. De manera que, la gráfica de y = f( x + h) se puede obtener de la gráfica de y = f(x) al trasladar horizontalmente la gráfica de y = f(x), h unidades hacia la izquierda si h es positiva y h unidades hacia la derecha si h es negativa.
Ejemplos para discusión:
1) Dibuja las gráficas de
2) Dibuja las gráficas de
; función idéntica
La función identidad puede describirse de la forma siguiente:
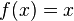 de
de  en
en  tiene como representación gráfica en el eje de coordenadas la línea recta que cruza el origen subiendo en un ángulo de 45° hacia la derecha.
tiene como representación gráfica en el eje de coordenadas la línea recta que cruza el origen subiendo en un ángulo de 45° hacia la derecha.
La función identidad en (el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación r = θ: una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.
(el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación r = θ: una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.
La función identidad en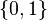 es la doble negación, expresada por
es la doble negación, expresada por 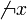
[editar] Ejemplos
La función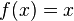 de
de  en
en  tiene como representación gráfica en el eje de coordenadas la línea recta que cruza el origen subiendo en un ángulo de 45° hacia la derecha.
tiene como representación gráfica en el eje de coordenadas la línea recta que cruza el origen subiendo en un ángulo de 45° hacia la derecha.La función identidad en
 (el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación r = θ: una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.
(el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación r = θ: una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.La función identidad en
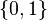 es la doble negación, expresada por
es la doble negación, expresada por 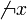
funciones reales de una variable real
La ley que relaciona el valor del área de un cuadrado con la longitud de su lado es una función. Sabemos que la expresión que nos relacionas ambas variables es  .
.
Observa que dependiendo del valor del lado del cuadrado vamos a obtener distintos valores en el área del mismo. Así, aparece una variable que no depende de nada (variable independiente: la l) y otra que si depende de los valores elegidos en la l (variable independiente: la A). Puedes pues construir una tabla con algunos valores:
Su recorrido es también el conjunto de todos los números positivos pues un área no puede ser negativa. Además siempre existe un cuadrado que tenga por área cualquier número positivo (bastará construir un cuadrado cuyo lado sea la raíz cuadrada del área elegida).
2.- Cualquier expresión del tipo y=f(x) de las estudiadas en cursos anteriores representa una función real de variable real.
Definición
Definimos función de x en y como toda aplicación (regla, criterio perfectamente definido), que a un número x (variable independiente), le hace corresponder un número y (y solo uno llamado variable dependiente).
De una manera más rigurosa: Definición
Se llama función real de variable real a toda aplicación f de un subconjunto no vacío S de R en R
Una función real está definida, en general, por una ley o criterio que se puede expresar por una fórmula matemática. La variable x recibe el nombre de variable independiente y la y o f(x) variable dependiente o imagen. Ejemplos
Calcula la imagen de los números 0, 1, 2, y 10 en las siguientes funciones: 
Observa que dependiendo del valor del lado del cuadrado vamos a obtener distintos valores en el área del mismo. Así, aparece una variable que no depende de nada (variable independiente: la l) y otra que si depende de los valores elegidos en la l (variable independiente: la A). Puedes pues construir una tabla con algunos valores:
l | A |
1 | 1 |
2 | 4 |
10 | 100 |
1/2 | 1/4 |
0,5 | 0,25 |
Su recorrido es también el conjunto de todos los números positivos pues un área no puede ser negativa. Además siempre existe un cuadrado que tenga por área cualquier número positivo (bastará construir un cuadrado cuyo lado sea la raíz cuadrada del área elegida).
2.- Cualquier expresión del tipo y=f(x) de las estudiadas en cursos anteriores representa una función real de variable real.
Definición
De una manera más rigurosa:
Una función real está definida, en general, por una ley o criterio que se puede expresar por una fórmula matemática. La variable x recibe el nombre de variable independiente y la y o f(x) variable dependiente o imagen.

reconoce la función constante
se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable. Se la representa de la forma:
Si un polinomio general, que tiene la forma:
Si un polinomio general, que tiene la forma:
función inversa
Se llama función inversa o reciproca de f a otra función f−1 que cumple que:
Si f(a) = b, entonces f−1(b) = a.

Podemos observar que:
El dominio de f−1 es el recorrido de f.
El recorrido de f−1 es el dominio de f.
Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.
Si dos funciones son inversas su composición es la función identidad.
f o f -1 = f -1 o f = x
Las gráficas de f y f -1 son simétricas respecto de la bisectriz del primer y tercer cuadrante.

Hay que distinguir entre la función inversa, f−1(x), y la inversa de una función,  .
.
Cálculo de la función inversa
1Se escribe la ecuación de la función con x e y.
2Se despeja la variable x en función de la variable y.
3Se intercambian las variables.
Calcular la función inversa de:
Suscribirse a:
Entradas (Atom)